This is Part 2 of looking at statistics for how likely various start-generation methods are to qualify you for desired classes in early D&D (partly inspired by our recent chat on Wandering DMs). Last time we looked at stat-generation in OD&D (3d6-in-order, maybe with a few point-swaps allowed) and the various sub-classes presented in supplemental material (ultimately resulting in the same list of classes that appear in AD&D). Here we'll look at the AD&D game and its very different matrix of possibilities for generating ability scores, and the ways it overhauled those classes and requirements.
A few reminders of ground rules: We're just looking at entry possibilities for single-classed humans, not considering demi-humans with racial adjustments, multi-class combinations, etc. Statistics were generated by Monte Carlo-type simulations from a C++ program (and spot-hand-checked in a few cases and against other resources). Today's entry is only dealing with rules as presented in the 1E AD&D PHB/DMG -- rules changes from 1E Unearthed Arcana (6 years later), will be considered in a follow-up post.
Ability Generation Methods
A wrinkle in the publication history of AD&D is that PHB came out in 1978, and it gave no rule for how players should generate ability scores -- it's one of several things locked away in the DMG ("The referee has several methods of how this random number generation should be accomplished to him or her in the DUNGEON MASTERS GUIDE"; PHB p. 9). And the DMG didn't come out until a year later, in 1979. So I'm assuming in the intervening year players were still using the OD&D 3d6-in-order method by default?
When the AD&D DMG did finally appear, Gygax specifically calls out using straight-3d6 as a bad idea in these rules (p. 11):
While it is possible to generate some fairly playable characters by rolling 3d6, there is often an extended period of attempts at finding a suitable one due to quirks of the dice. Furthermore, these rather marginal characters tend to have short life expectancy -- which tends to discourage new players, as does having to make do with some character of a race and/or class which he or she really can't or won't identify with.
He then offers four alternative methods that can be used for the AD&D game, as shown below:
I'll rephrase those slightly. For comparison sake, I'll also include the OD&D method as "Method
0" to see how it stacks up against the AD&D methods. And note that
while the book identifies them with
Roman numerals, I'll use Arabic identifiers here, to more easily synch
with
my C++ code and its customary output:
- Method 0:
Roll 3d6 in order for the six abilities.
(The OD&D rule, of course, not actually in AD&D for player characters.)
- Method 1:
Roll 4d6 and drop the lowest die, six times, and order to taste. (This
is the default rule from 1E all the way to 5E -- and most likely 6E as
well, which won't be changing that element, according to a draft Character Origins document released by WOTC the other week.)
- Method 2: Roll 3d6 twelve times, take the best six, and order to taste.
- Method 3: Roll 3d6 six times for each ability, and take the best of the six in each case.
- Method 4:
Roll up twelve separate characters using 3d6 in order (i.e., as per the
OD&D Method 0). Pick your favorite of the twelve characters.
(Yes, Virginia, there is a "Method 5" variant from the later Unearthed Arcana, but we'll address that next time.)
One thing to note is that the AD&D methods require exponentially more dice-rolling as one proceeds to the later methods:
And, here are the base-level descriptive statistics differentiating the various methods:
We
see that Method 3 produces notably higher scores than the other methods
-- it has an average of 14, while the other AD&D methods all hover
around 12 to 13. Method 3 is also the most reliable in that it has the
lowest standard deviation (e.g., the gold-standard for modern portfolio
theory). Yet, we'll see later that, due to its lack of re-ordering to taste, Method 3 is not necessarily the best method in regards to the question of qualifying for certain classes.
I'll also note that for Method 4, I assumed that from
the dozen characters generated, you pick the one with the highest
sum (or average) of abilities -- although that too may not be the way it
actually gets played, depending on the which character class one
most desires. Again, we'll see the results of that further below.
Classes and Requirements
Recall that OD&D had no ability score requirements for the core classes in the LBBs, but did start using that as a mechanic to gatekeep the various sub-classes added in supplemental works. AD&D generally raised all of the requirements, in particular, instituting that any class had to have a score of at least 9 in their prime requisite (explicitly counter to the OD&D table of ability modifiers). Higher scores were required for sub-classes and even nonhuman racial choices.
And there's a further wrinkle in the fine print of the ability score rules that's easy to overlook: each of the character ability tables has a note for the 3-5 score range that restricts a character to only one particular class. For example, in the Strength table (PHB p. 9), it says, "Here or lower the character can only be a magic-user". Low Intelligence restricts you to Fighter; low Wisdom to Thief; and low Dexterity to Cleric -- while low Constitution mandates the Illusionist subclass, and terminally low Charisma restricts the character to being an Assassin.
So this results in an implicit "hopeless character" rule that requires re-rolling an AD&D character in some cases -- if you get more than one ability score in the 3-5 range, then the conflicting class mandates are not mutually satisfiable, and the character cannot pick any class at all. This gets echoed years later in the rules for D&D Basic; for example, Mentzer writes (Basic D&D Players Manual, p. 48), "If two or more Ability Scores are less than 6, the character may have problems later on. This type of character should also be discarded, unless the DM says otherwise." This is just a rephrasing of the same implied criteria in the AD&D PHB. (Also, I'm guessing that the 5E "no hidden rules!" dogma was motivated precisely in response to Gygaxian mechanics like this.)
This is a place where the otherwise excellent analysis of AD&D class access at Athenopolis.net made a misstep, I think -- they show the default ability minima to be 3 unless otherwise stated, when it's actually 6 by the AD&D ability tables (excepting precisely one 3 allowed for any given class). Fortunately, we'll see that in most practical cases this makes for only a small difference in our results.
A further interpretive assumption I'll make is that these very-low-score restrictions permit entry into an associated sub-class, unless otherwise stated. For example, if you have a 3 in Strength, such that the table explicitly says you can only be a Magic-User, then I'll assume you could alternatively be an Illusionist (if your other scores qualify). But that won't make a detectable difference either way you read this corner-case issue.
In summary, here are the requirements for the various classes in the 1E AD&D PHB as I see them:
Qualification Chances
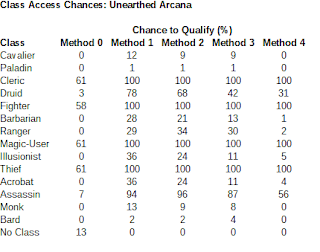
So here's what our simulator reports for qualification probabilities across the various AD&D stat-generation methods. Numbers are all percentages, rounded to the nearest whole number. At the bottom there's an extra row denoted "No Class" for those unfortunates trapped by having more than one very low ability score, as described above. Classes are presented here in the same order as tables in the AD&D PHB:
Note that the 0's and 100's in this table are all the result of rounding; nothing is guaranteed, but you get very close in many cases. In light of the inflated AD&D requirements, we see that we really had to progress to something other than the OD&D Method 0; many of the classes would be effectively impossible by that method (less than a half-percent chance to be accepted), our primary four classes now only have about 60% pass rate, and 13% of all characters are "hopeless" and can't enter any class.
Note that those primary classes, rolled under the OD&D method but with AD&D requirements, are really the only places where our numbers notably differ from those of Athenopolis.net (they show acceptance values about 10% higher than what we have here). These are the classes where the 6-not-3 default requirement affects the most abilities. Of course, this whole column is purely theoretical, because Method 0 is nowhere officially supported by AD&D -- unless we consider the one-year window between PHB and DMG when that may have been still practiced? All the other entries are usually less than a 1% difference in our mutual results.
By using any of the official AD&D methods, we see that the primary classes return back to near certainties (for example, you're 99.8% likely to qualify for a cleric, fighter, magic-user, or thief, using Method 1). It's actually Method 1 that generally has the best chances to qualify for a given subclass, with Method 2 generally a close runner-up -- these are the two methods that allow re-ordering abilities to the player's taste. If you're stuck with abilities in a predetermined order, as in Methods 3 and 4, regardless of how much they otherwise boost the numbers -- remember, it's Method 3 that generates the highest scores on average -- it's fairly unlikely you'll have the exact profile you need, and qualification rates are a lot lower as a result. Method 4 in particular, using a stack of a dozen Method 0-OD&D characters, is very bad in this regard (showing 0, 1, or 2 percent for a number of classes).
Let's focus mostly on that prominent Method 1 (there's a reason it was carried forward as the starting point for all later editions, while the other methods were mostly abandoned). It boosts previously very rare subclasses to more common occurrences: for example, about one-quarter of all characters qualify to be a Paladin or Ranger (compare to less than 2% in OD&D). Druids go from 6% to 78%. Illusionist was 9%, now it's 36%. Assassins scaled up from 5% to 94% (and, again, are even required in the case of very low Charisma).
One thing that jumps out at many of us when we first see this is that the Monk is actually even harder to qualify for than the much-treasured Paladin class -- it's about half the rate of Paladin success in both Methods 1 and 2. But the truth is that getting 3 scores of 15+ is harder than getting a single score of 17+, which are the critical requirements in both OD&D and AD&D. It's probability, kids!
Then you have the totally overhauled Bard class (also removed to PHB Appendix II), which is the only class in the book with explicit minimum requirements for all 6 ability scores (needing at least four 15's, one 12, and a 10). This is an overwhelmingly challenging prospect, with success rates of only 2% for Methods 1 and 2 (but oddly 4% with Method 3, making Bards the only class that Method 3 is better for). Contrast this with the gentle requirements in the OD&D version which gave it the highest acceptance rates for any subclass there.
Forgive me for a rabbit-hole on further weirdness with the Bard regarding the topic at hand: As any AD&D player knows, you can't start as a Bard (unlike the OD&D version); you have to starts as a Fighter, get to at least 5th level, switch to a Thief, progress to at least 6th level, and then switch to the actual Bard super-class (in the direction of what 3E would later identify as "prestige classes" in immense profusion). Note that among the several 15's the text says a Bard needs for their abilities, one of those is Dexterity. But: the core rule for humans switching classes ("The Character With Two Classes", PHB p. 33) dictates that one needs a 17 or 18 in the prime requisite of the class you're switching into -- in this case, Dexterity, when you make your first switch to Thief. So how do those rules interact? I can see arguments for (1) the core switch-class mechanic still apples, so you have a "hidden rule" that a Bard really needs Dexterity of 17+, or (2) the specific description of the Bard class overrides that, and Bards-to-be have a special allowance in their class switching. With that latter rule I can imagine a case where some rules-lawyer says they're aiming for Bard, double-classes as Fighter and Thief with only Dex 15, but then later reneges (a very niche case, to be sure). Nonetheless, for this analysis I've gone with option (2) and assumed the Bard truly needs only Dex 15. (If you instead rule that they really require Dex 17, then the chance to create one drops to approximately 1% for Methods 1 to 3, and less than 0.01% for Method 4.)
Finally, as we see in the last row, the "hopeless" no-class possibility that we outlined above is really a nonissue using any of the AD&D generation methods. With Method I the chance of this happening is only 0.06% (6 times in every 10,000 characters rolled), and with other methods it's even lower (less than 0.01% each).
What surprising things do you see in those results? Would this analysis make you re-think what method(s) you'd want to use in a new AD&D game? Next time: in what ways Unearthed Arcana stirred stuff up a few years later.
























.jpg)















