Why Did Natural 20's Become Automatic Hits?

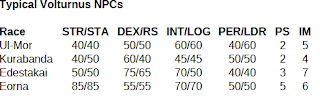
Here's an observation I just made, that came up from a friend's question about the 1E AD&D rules for a big project they're working on. Ultimately this highlights the less-than-optimal state of editing in those books. You may know that 1E AD&D did not have a "natural 20 always hits" rule, but it did show a repeating sequence of 20's in the to-hit tables (DMG p. 74-75):

A few pages later, there's a paragraph-long note highlighting the status of those repeating 20's (p. 82):

Of course, I've read and relied on this paragraph many times over the decades. But suddenly I found myself having trouble parsing the language re: "Should any DM find that this system offends his or her sensibilities, the following modification is suggested..." Specifically, what's the other (default) option for interpretation that is being modified here?

Here's the thing: This supposed "modification" is the mechanic you get anyway, based on an earlier core rule for how modifiers are applied to attack rolls. Note the end of this section alludes to the special "20" entries on the combat tables, and how this important rule is meant to interface with that (p. 70);

Playing by the rules as written, this establishes a key factor that since the attack tables are not entirely formed by a linear progression (due to the pattern-breaking flat spot of 20's), you really need to use those tables directly, and they can't be translated into elementary arithmetic formulas. You must apply modifiers to the row of the table, and not the die-roll, which would easily let you jump over the repeated 20s (to the benefit of either side depending on direction of modifier).

But that makes the "modification" on p. 82 redundant: Once you've applied all modifiers to the row of the table (per base rule p. 70), then the entry you look up is precisely the target you need on the die. There are no more bonuses to apply, and so a "20" means nothing except that you need to see a real, actual, natural 20 on the die. (Arguably we shouldn't even see scores of 21+ in the table, because by definition they're unhittable per this rule.)

So effectively the need to apply modifiers pre-die-roll has been presented to us twice -- Once on p. 70, and again on p. 82. It's just that the p. 82 text neglects the earlier rule, incorrectly takes an apply-modifiers-to-die-roll mechanic as the default, and so delivers the same rule again as a "modification".

AD&D 2nd Edition

Again, AD&D 1st Edition does not have a "natural 20 always hits" rule; the repeated 20s go in that direction, but the rules explicitly call out that some very well-defended types should be unhittable (parenthetical on p. 70: "At some point, the upwards armor class adjustment could also make such opponents virtually invulnerable, but this is less likely and not necessarily undesirable").

The first time that "natural 20 always hits" rule appeared was in AD&D 2nd Edition (DMG p. 53, here justified with, "There are no sure things, good or bad, in the unpredictable chaos of combat situations"). Those rules don't even have attack matrices like 1E did (it's switched entirely to use of formulaic THACO as a core rule), so there aren't any repeated-20s to do that job anyway.

D&D 3rd Edition

3rd Edition D&D (and everything from 2nd Edition on) keeps the core rule of "natural 20 always hits". However, the developers seemed not entirely comfortable with this, and/or they were looking back at the 1E rules, because in the DMG there's a variant presented:

This variant suggests that we treat  natural-20 not as an automatic hit, but mathematically as if a 30 had been rolled. This does the same kind of job as the 1E rule: some things are still unhittable, but there's a big extended "flat spot" of targets vulnerable to a natural-20 roll, and only that. In this case the flat spot is extended by an extra 10 pips (that is, 11 AC values hittable only by natural 20). 

Note that we could do the same thing in 1E/2E while avoiding either the table matrix or automatic hits. If we say that a natural-20 on the die counts as 25, then mathematically we get the exact same flat spot of probability that's shown in the 1E tables (a total of 6 ACs hittable only by natural-20). 

Original and Basic D&D

It bears noting that Original D&D had no ramp-down on the tails of its attack tables; the tables there show a progression all the way down to a "1" needed to hit (i.e., automatic hit), although armor doesn't go high enough to get into the "20" vicinity. On the other hand, the Swords & Spells supplement does extend those tables, and a single step past 5% to hit, the chance becomes 0% (i.e., automatic miss). The Holmes Basic tables show the same thing as OD&D, with some hits allowed on a roll of "1".

On the other hand, the Moldvay/Cook Basic Set (1981) does assert that, "a roll of 20 will always hit, and a roll of 1 will always miss" (p. B25), this being eight years before Cook inserted the same rule into 2E AD&D.

Effect in Reality

In theory, Gygax's intuition that the extreme-cases should switch to immunity-from-attacks gradually, not abruptly, is totally correct. If we look at data for shooting accuracy, for example, it's universal that the graphs look like an "S-curve", with a flatter spot of probability at either end as it tends to either 0% or 100% accuracy. Mathematically we call these (or really the inverse, i.e., a miss-chart) sigmoid curves, and among other things they represent the integral of any probability function (i.e., a cumulative distribution function). One such chart (from Litz, "Accuracy and Precision for Long Range Shooting", Ch. 7):

Based on an analysis we've done here previously (see very end of final chart), if you assume normal-distribution variance in accuracy, and 5% steps in the middle of the curve, then we might actually think that a tail "flat spot" of around 10 steps before shots become impossible is reasonable (i.e., the 3E rule might be better than 1E).

However, it's nontrivial to find examples in classic D&D where there's any practical difference between the (realistic) flat-spot distribution tail, versus the (super simple) natural-20-always-hits rule. The most obvious one would be in a wargame/battlefield situation, with a company of normal archers shooting at some fantastic type with AC 0 or better at long range (e.g.: some devils, tougher dragons, or a Lord in +1 plate and shield). Under the 1E rule, these figures are totally invulnerable (0% to hit); whereas under the 2E rule, we can expect them to be cut down in a single round by a sufficient number of archers (say, 100 or more at 5% to hit). Think about how much of a difference that makes in your game, say, for army commanders and superheroes on the field of battle.

So for most standard D&D dungeon-crawling encounters with PCs roughly matched to the opponents they face, we don't expect to observe any effective difference between the two rule options. Approximating the real-life "S-curve" effect by saying "natural 20 always hits" is actually a pretty reasonable rule simplification. In my own OED house rules I now do that, with a caveat that "DM rules on impossible cases".

Star Frontiers: Volturnus Racial Abilities

As you'll know if you followed the spring season of Dan's Olde Time Minis Show, I've been playing the classic Star Frontiers game all this year, and enjoying it immensely. To me, running a roll-low percentile system seems like a breath of fresh air. My players have called out as highlight the interesting intelligent races and cultures for both PCs, and in the standard Volturnus campaign, the alien NPCs.

Those Volturnus alien species seem smartly and loving crafted, with dense one-or-two page briefings on each of their cultures. However, one thing was overlooked: as important as they are to the ongoing campaign, no ability score modifiers are presented for them, as they are for the PC races. How strong is the average Ul-Mor, anyway?

Fortunately, we can deduce what they should be, because in the climactic "Battle of Volturnus" in the final module (SF 2: Starspawn of Volturnus, Zeta Section), stats for collective mass units of each race are presented, which presumably match the "Typical NPC" profile for each type. This assumption is solidified by the opposition Sathar unit stats indeed being a copy of their Typical NPC stats from the core rulebook (p. 59). Note that up until that climax, variable stats are given for every individual that appears, which is not so helpful. Let's compute.

Sathar

First, let's discuss the Sathar. This investigation actually uncovers an error in the core rules. Here's the typical Sathar stat block, as it appears in module SF 2. This is repeated identically in each of four encounters (on p. 26, 27, 28, and 29), and it also matches the Typical NPC table in the Expanded rules p. 59, as well as the Referee's Screen:

Now, despite that agreement across multiple pages and products, it actually contradicts the Sathar ability modifiers in the core rules (p. 10). Given that the average base ability score starts at 45, the p. 10 text says that Sathar STR/STA should be +0, while the INT/LOG should be –5 (so, respectively, an average of 45 and 40). But that's flipped-flopped compared to what's in the Typical NPC stat blocks.

Apparently this must have been a design edit that didn't fully matriculate everywhere in the rulebook (DRY violation). Thinking about it, I prefer what we see in the Typical NPC stat blocks. While Sathar are long wormy creatures, they're less massive than most other types (arguing for low STR/STA), but are infamous as ingenious spacefaring technologists, warmongers, and cunning saboteurs (so probably not low INT/LOG). In my book, I've scratched out the p. 10 modifiers and made them match the typical stat blocks -- and hence don't have to edit all those stat blocks the many other places they appear.

So the duly-corrected Sathar ability modifiers are: STR/STA –5, DEX/RS –5, INT/LOG +0, PER/LDR +10 (and then a required 10-point shift from PER to LDR). 

Ul-Mor

The Zeta-section stats for the Ul-Mor cavalry look like this (SF 2, p. 29):

From this we can deduce these ability modifiers: STR/STA –5, DEX/RS +5, INT/LOG +15, PER/LDR +5 (and then like the Sathar, with a required 10-point shift from PER to LDR).

Kurabanda

A squadron of Kurabanda are given these common stats (SF 2, p. 23):

So their ability modifiers should be: STR/STA +0, DEX/RS +5, INT/LOG +0, PER/LDR +5 (with a standard shift of 5-points from STR to STA, and another 5-point shift from RS to DEX).

Edestakai

The Edestakai infantry get these stats (SF 2, p. 27; and repeated in SF 1, p. 12):

These resolve to the following modifiers: STR/STA +5, DEX/RS +25, INT/LOG +15, PER/LDR –5 (with a required 5-point shift from RS to DEX, and a 10-point shift from LOG to INT).

Eorna

A group of Eorna skirmishers get these stats (SF 2, p. 28):

Now, there's a glitch here because the odd 5-point difference between STR and STA can't be recreated by the standard character generation rules. Also, the PS (punching score) is in error; for a STR of 80, it should only be 4 (although any STR higher than that would indeed produce a 5). A similar error pops in a number of the various Eorna stats in SF 1, p. 29. To resolve these, I'd suggest that the STR really should be 85 -- matching the STA score, and making the PS value then correct. 

So given that, the Eorna ability modifiers should be: STR/STA +40, DEX/RS +10, INT/LOG +25, PER/LDR +5.

Conclusion

It's nice to finally have those visible for convenience and comparison.

One thing that we immediately notice is that whereas for the Star Frontiers PC races, the ability modifiers are all perfectly balanced (sum to zero for each race) -- for the Volturnus races, that is definitely not the case, and they trend increasingly beefy as the campaign evolves, with generally big bonuses and few to no penalties. I think that's fine for exotic aliens that don't need to be balanced as player character options, and can present as powerful and dangerous friends and/or enemies.

A related detail that's still missing is, as far as I can tell, no movement profiles are ever given for any of these races. That would be nice to have.

And another question one might ask is: What about stats for the Mechanon collective? Well, unfortunately, they're never given character-type ability stats at any point in the campaign -- not even a single one, as far as I can tell. Oddly, they appear as a PC race in the Zebulon's Guide supplement, and get a line in the expanded "Typical NPCs" table (p. 5), but are still missing from the racial ability modifier table (same page). Overall, I think that book is highly suspect and don't trust it for anything.

Finally, here's a consolidated table of Typical NPC stats (of which we know) for the Volturnus races:

Until next time, don't forget to take your vitasalt pills, kids.

Star Frontiers Miniatures Revisited

Hey, it's been quiet around here lately... too quiet. Maybe we can get some new D&D material up soon.

In the meantime, hopefully you've had a chance to catch some of Dan's Olde Time Minis Show over on the Wandering DMs YouTube channel? For Season 1 I dug into collecting & duplicating the 1980's Star Frontiers PC miniatures, which I'd never had a chance to do before -- partly inspired by the classic Star Frontiers Volturnus campaign that I'm currently running for new players. We're having a blast! 

Of course, I'm building up my collection by making rubber molds by hand and casting new miniatures with lead-based miniature metal in my kitchen on the livestream. There have been a few exciting moments, to be sure. Here's the first episode:

And ultimately here's the entire lot of what we produced and painted over that first season:

For more Star Frontiers miniature production, you can look into the distant past on this blog where I started out manufacturing a sizable fleet of the Knights Hawks spaceship miniatures. Just don't let your Dralasites lick them!

Fearful Ends Now on Kickstarter

The long-time passion project of my Wandering DMs partner Paul Siegel is currently funding on Kickstarter!

Fearful Ends is a rules-light, story-centric roleplaying system for horror themed games. It features nihilistic stories about characters discovering impossible horrors. It aims to allow players to roleplay characters that experience mental or emotional collapse in a safe play environment that neither stigmatizes nor sensationalizes mental illness. 

We've been playing and refining Paul's system for horror games for a bunch of years, and it really runs well. I've even GM'd a session of it myself with a custom scenario very successfully, without needing to be a deep expert in this flavor of RPG. Easy to pick up and learn, and we always have a great time with it.

Join the Fearful Ends Kickstarter today!

40 Years of the D&D Cartoon

The D&D cartoon first appeared on CBS 40 years ago this week! Man, 1983-1984 were really great years for our hobby.

Here's a link to the blog and an hourlong video interview by Mark Evanier, who wrote the pilot script and series bible"

News From Me (Mark Evanier)

How Much Weight Can a Horse Carry in D&D?

I've vaguely known for a long time that there was some essential problem with the system for horse encumbrance in early D&D (O/AD&D). But I hadn't personally done the accounting to pinpoint where the issue was; I recently went on a deep dive on that point. Big thanks to the folks on the Wandering DMs Discord server for pointing out the problem in OED and helping me think through this reasonably.

Original D&D

To the side here is the page of encumbrance rules from OD&D (Vol-1, p. 15). Once again I'm struck by the overall completeness of the Original Dungeons & Dragons rules: whatever its other faults, everything you could possibly need to know about D&D encumbrance is included on this one digest-sized page. This includes: the weight of weapons and armor, helmets and shields, bows and arrows, miscellaneous gear, coins of any type, gems and jewelry, magical treasures, movement categories, container carrying capacities, saddles and barding for horses, and the weight of an average man. Plus a complete example. This compares extremely favorably to what came later: in AD&D, you'd need to look in at least four separate books, published over eight years time, to put all the equivalent information back together. (This complication makes it nontrivial to do the desired accounting as I wanted for AD&D, below).

So, here's the accounting for light, medium, and heavy lancer cavalry, under reasonable assumptions, according to the OD&D rules.

Here's some notes & observations on that.

• Horses are only given a single maximum load limit (in the Vol-2 monster entry): by type, 3000, 3750, and 4500 coins. These values are vaguely reasonable: real-world research frequently pegs 30% body weight as the point where horse gait performance starts to experimentally drop off (e.g., Wikipedia: "horses can carry approximately 30% of their weight"). If we take very round estimates for horse weight of 1000-1250-1500 pounds, and compute 30% of those, then we get exactly the load limits shown here.
• The weight of men given, 175 pounds, is roughly equal to the average weight of men in the U.S. in the era of publication (173.4 pounds, per NHANES I, 1971-74 from the CDC; compare to S&P's estimate for medieval Swiss men, 71.7 kg = 158.1 pounds).
• The weights for arms & armor seem high, like, around double the weights based on real-world examples (possibly more on that later). 
• These rules only give one type each for a saddle, barding, shield, helmet, lance, and one-handed sword, so these are common across each cavalry type.
  
• Following the listing for bandit men et. al. (in Vol-2), the expectation is that heavy horse are barded, but light and medium horse are not.
• In particular, the barding weight (75 pounds) is reasonable; compare to Wikipedia ("barding, or horse armour, rarely weighed more than 70 pounds"). Several examples at the Met Museum weigh in at around 90 pounds. 
  

Conclusions for OD&D:

• The fully kitted-out cavalryman weighs in nicely within the load limit given for each type of horse (indicated by green highlight in table).
• Moreover, the gear for each type is greater than or equal to the limit for the next lower type -- implying that for medium kit-out you want the medium horse, and for heavy kit-out you really need the heavy horse. (Arguably, you could just barely use a light horse for medium kit; but let's ignore that wrinkle for now.)
• In addition, if we look at the gear on the man alone (perhaps if they have to fight on foot), these weights also synch up perfectly with the encumbrance tiers for men (given as 750-1000-1500 coins). Respectively, each is just barely within the window for light, medium, and heavy loads for men (12-9-6 inch movement tiers).
• Overall -- this is excellent, coherent game system design. All the parts work together to generate the expected & desired results. The numbers are within the ballpark of modern real-world research. It has the sign of someone who paid close attention to both historical details and good wargame design.
  

Advanced D&D

Now for a different story. First of all, doing a similar accounting for AD&D is a lot more work, because (as noted above), the equivalent information is spread all over at least four different books. To wit:

• The PHB (1977) has melee weapon weights (p. 37), and elsewhere movement thresholds for men (p. 101).
• The DMG (1979) has armor & shield weights (p. 27), and in Appendix O (p. 225), most other weights for miscellaneous gear, bows & arrows, helmets, saddles, etc.
• Container carrying capacities could only be found if you looked in the AD&D Player Character Record Sheets product (1980). 
  
• The specifications for barding weren't given until an article by Gygax in Dragon Magazine #74 (1983), and then reprinted in Unearthed Arcana (1985).

You can take this as a case study of my thesis that there was a lot of key stuff in OD&D that was haphazardly copied or lost in the transition to AD&D, making it a lot more cryptic and mysterious than it needed to be. Anyway, putting it all together we can get the accounting for cavalry weights in AD&D:

 Observations here:

• In the AD&D Monster Manual, horses get two load categories: light (full-speed; approximately equal to the OD&D limits), and heavy (half-speed; about double the light load). That's arguably reasonable.
  
• The average male human weight of 175 pounds is reiterated in the table on DMG p. 102, so we use that again in our spreadsheet.
  
• The weight for arms & armor are generally reduced, pulling them more towards real-world scales, as far as I can tell.
• The Advanced D&D ruleset gives distinctions to different types of saddles, barding, shields, helmets, lances, and swords -- so I've indicated the expected selection for each.
• In particular, DMG p. 31 describes medium horsemen as "similar to heavy cavalry", so when necessary I picked the heavier version of the gear (saddle, shield, helmet).
• The AD&D Monster Manual makes no reference to expected barding anywhere in the book (contrast with OD&D above). So are we to assume that light cavalry always use the leather barding, medium chain, and heavy plate, as provided in the equipment list? That would be my best guess of the intent (despite it being ahistorical to my knowledge) -- so that's what I've entered for each type.
• Strangely, Gygax has massively increased the weight of barding to a completely ludicrous level (noted by orange warning lights above). Even the leather barding is more than double the weight of barding in OD&D. Plate barding is more than quintuple the heaviest historical example I could find -- on its own, maxing out the first-tier load limit of the heavy horse. (!)
  

Conclusions for AD&D:

• The fully-kitted cavalrymen are all significantly over the limit for expected full-speed horse movement. In particular, the heavy horseman is far over the maximum limit for the heavy horse, and cannot move at all by the letter of these rules. The medium horseman is only 3 pounds away from the same thing. (Noted by yellow & red highlights.)
• Apart from the barding issue, looking at the men alone (i.e., off the horse), there is a similar problem. The load limits for average-strength men have been reduced by an order of about a half (35-70-105 pounds in the PHB), and the light & medium men are over the expected limits for the first two categories. (Despite this reduction being maybe real-world reasonable, it outpaced the reduction in arms & armor weight to drop the men into slower categories.)
• Overall -- this design is simply broken. The primary problem is the unwarranted and inexplicable inflation in barding weights (which, again, renders the heavy horseman immobilized). But more generally, the fragmentation of where the encumbrance rules are located (scattered all over many books) is echoed in the design decisions being unsynchronized, and have produced a fundamentally incoherent system.
  

Further Discussion

Obviously, this is another instance where the Original D&D system runs the table on the later Advanced D&D system. It's really puzzling how the latter system was allowed to get so fragmented, so quickly, as to produce results like this.

I suppose one could argue that the light and medium horse types shouldn't be expected to wear barding -- despite a move-limit table in Dragon #74/Unearthed Arcana showing them in it (a table which doesn't make any sense, because the raw weight has already slowed the horse down more that the table shows for armor max moves). At the very least, you have to observe that plate barding is useless, because it and a heavy horseman are more than any horse can bear.

Of course, a lot of people don't want to use encumbrance rules at all. If you've read this blog before you're likely aware of my argument that scaling the weight units to individual coins was too fine-grained, and juggling all the big numbers is a major part of the headache. So I prefer using a bigger unit like historical stone weights, which (usually) makes the calculations easier to estimate and add up.

Based on our research on real-world horse carrying capacity, I'm confident that the 30% body weight number is a solid value to use before horse speed drops off (see short bibliography below). And aligned with patron feedback, I've become convinced that the 20% body weight number cited in a lot of modern horse-riding articles represents a very conservative rule-of-thumb, trying to be painstakingly humane, with a large safety buffer built in (i.e., not representing medieval workloads). For the OED House Rules we plan to use a round guideline of 1/3 and 2/3 body weight for the light and heavy load thresholds. This represents a revision to this prior article.

Finally, I seem to recall a letter or article in Dragon Magazine that pointed out the problem with AD&D horse encumbrance, in particular, that a heavy horseman couldn't move at all. But I can't remember which issue, and asking around online to date hasn't gotten any answers. Do you know of such an issue?

Answered: In the comments below, jbeltman found the letter we were looking for -- in Dragon Magazine #118 (February 1987), Forum p. 6, by David Carl Argall (of La Puente, CA). Huge thanks to jbeltman for that!

Bibliography

• Bukhari, Syed SUH, Alan G. McElligott, and Rebecca SV Parkes. "Quantifying the impact of mounted load carrying on equids: a review." Animals 11.5 (2021): 1333. -- This is a really great, recent review of all the research to date around the issue of horse carrying capacity.
• Matsuura, et. al. . Various articles (2012, 2013, 2016, 2018, etc.) -- Matsuura runs a lab in Japan that studies different horse breeds, and keeps coming up with a number close to 30% body weight for the point where any statistical dropoff in performance can be observed.
• Wickler, S. J., et al. "Effect of load on preferred speed and cost of transport." Journal of Applied Physiology 90.4 (2001): 1548-1551. -- Wickler loaded seven Arabian horses with about 20% body weight burdens, let them walk freely with no rider or lead, and found only about a 5% drop in the speed at which they wanted to walk.

Here's a spreadsheet (ODS) with the tables above if you want to play around with them.

Solving Chainmail Jousting

Last year I wrote an academic paper formally solving Gary Gygax's Jousting game, as it appears in the original edition of Chainmail: Rules for medieval miniatures (1971; and prior to that in The Domesday Book newsletter).

This paper was presented at a conference of the International Computer Games Association (ICGA), namely, Computers and Games 2022 (CG2022) -- and recently published in the Springer collected lecture notes for the conference. You can see the abstract here:

Collins, D.R. (2023). Solving Chainmail Jousting. In: Browne, C., Kishimoto, A., Schaeffer, J. (eds) Computers and Games. CG 2022. Lecture Notes in Computer Science, vol 13865. Springer, Cham. https://doi.org/10.1007/978-3-031-34017-8_4

Solving the game involves a mix of mathematical game theory principles and computer solving techniques. In brief, it turns out that there are 3 tentpole "best strategies" (Nash equilibria), involving a particular probabilistic selection of a handful of possible moves in the game. And for more sophisticated play, you can mix-and-match these three tentpoles in an infinite number of ways (all having an equivalent expected win payoff). One of the tentpole strategies is extremely simple, and possibly identifiable on inspection of the game matrix by a smart player; the others are more obscure.

Fortunately, the organizers of the conference record all of the presentations and make them publicly available on YouTube. Here's the session where I made my presentation (first in the block): it goes fast, as we only have 15 minutes each to speak. I'll let you watch below to see the three magic best strategies. Thanks to the organizers for giving me a platform to present these results!

(Note: If you're an entrant to the Jousting tournament at the GaryCon game convention, this won't help you win there; the rules context is significantly changed there in terms of the number of rides, point-scoring, end-game, restricted-ride rule, etc.)